
MATEMATIKA U DOBA KORONE
- On March 16, 2020
- By Natasa Tosic
- Comments Off on MATEMATIKA U DOBA KORONE
U jeku svetske pandemije virusa Covid-19, zdravstveni službenici i državni zvaničnici drže redovne konferencije za štampe, putem kojih nas obaveštavaju o aktuelnoj situaciji, broju zaraženih i merama koje trebamo preduzimati. Skoro u svakom obraćanju možemo čuti izraze kao što su geometrijska progresija, eksponencijalna kriva ili rast, matematička simulacija, funkcija rasta ili čujete kako se kaže da želimo da “spljoštimo krivu” širenja virusa. Kako bi razumeli ozbiljnost situacije pokušaćemo da vam pojasnimo neke matematičke termine, koji se u doba Korona virusa često koriste, a možda niste 100% sigurni šta znače.
Geometrijska progresija
U matematici geometrijska progresija je niz takvih brojeva da je količnik bilo koja dva uzastopna člana konstanta poznata kao odnos(količnik).
Geometrijski niz može biti zapisan kao:
aq°=a, aq¹=aq, aq², aq³…
gde je q ≠ 0, q odnos(količnik), dok je a prvi član niza.
Šta to praktično znači u okvirima pandemije virusa Covid-19.
Ukoliko jedan dan imate 4 zaražene osobe, od kojih svaka (ne pridžavajući se mera samoizolacije i ostalih mera prevencije) zarazi 2 nove osobe, sutra dan imamo 12 zaraženih (4 iz prvog dana i 8 novih), ukoliko sve zaražene osobe nastave slobodno da se ponašaju i zaraze svaka još po 2 nove, trećeg dana imamo 36 zaraženih. Ako tako nastavimo, četvrtog dana imamo 108, petog 324, šestog 972… ako pogledamo broj zaraženih kao jedan niz on izgleda ovako:
4, 12, 36, 108, 324, 972…
Ovaj niz predstavlja geometrijsku progresiju.

Pored geometrijske progresije, postoji i aritmetička progresija. Aritmetička progresija je niz brojeva takav da je razlika bilo koja dva uzastopna broja konstanta.
Na primer, niz 1, 2, 3, 4 … je aritmetička progresija sa zajedničkom razlikom 1.
Drugi primer: niz 3, 5, 7, 9, 11… je aritmetička progresija sa međusobnom razlikom 2.
Matematička funkcija
Po definiciji funkcija je jedan od osnovnih pojmova matematike, pojavljuje se u većini oblasti matematike. Funkcija ili preslikavanje je svako pridruživanje elemenata jednog skupa (domena), elementima drugog skupa (kodomena) pri čemu se svaki element skupa preslikava u tačno jedan element drugog skupa.
Kada znamo definiciju funkcije, možemo uzeti da u jednom skupu imamo broj zaraženih, a u drugom skupu vreme (odnosno dane). Po definiciji jedan element iz skupa “broj zaraženih” pridružujemo elementu iz skupa “vreme”. Na primer:

*Informacije sa sajta https://covid19.rs/
Sa funkcijama se srećete možda i češće nego što mislite. Funkcija se grafički predstavlja grafikom funkcije. Pa kad god imate grafički prikazane promene nekih vrednosti u toku vremena – vi gledate u funkciju.
U matematičkoj analizi najčešće se koriste funkcije realne promenljive. To je funkcija čiji je domen podskup skupa realnih brojeve R ili ceo skup R, a kodomen joj je R.
U zavisnosti od odnosa u kojima se nalaze vrednosti domena i kodomena definisani su razni tipovi realnih funkcija npr:

Eksponencijalna funkcija
Funkcija koja se često pominje u doba Korona virusa je eksponencijalna funkcija. Po definicji funkcija zadata formulom:
y = ax gde je a ∈ R, a > 0, a ≠ 1 se naziva eksponencijalna funkcija.
Eksponencijalna funkcija je interesantna za matematičko modeliranje zbog svojih osobina. Ona je monotono rastuća porastom nezavisne varijable x, gde se brzina rasta povećava kako raste x. Grafik eksponencijalne funkcije izgleda poprilično strmo, što na primer, ako funkcija predstavlja broj zaraženih u odnosu na vreme, treba da nam stavi do znanja da će broj zaraćenih vrlo brzo rasti.

Eksponencijalne funkcije se prirodno javljaju kao matematički modeli situacija u kojima je promena neke veličine proporcionalna toj veličini. Primeri su rast populacije, prirast biomase, raspadanje radioaktivnih stvari, itd. Slična je priroda razmnožavanja pojedinih bakterija koje bi, da ne uginu, približno istim tempom kojim se rađaju, eksponencijalnom eksplozijom, brzo preplavile Zemlju.
Za virus Covid-19, eksponencijalna funkcija je bitna, jer se njom prikazuje predviđanje broja zaraženih. Ova predviđanja su vrlo realna ukoliko se ljudi ne pridržavaju mera karantina, samoizloacije i drugih propisanih mera koje utiču na usporavanje rasta broja zaraženih.

Spljoštene krive
Možda ste čuli da se u Srbiji uvodi vanredno stanje i posebne mere Vlade u ograničavanju kretanja, a sve u cilju usporavanja rasta broja zaraženih. U žargonu ćete čuti izjave moramo da “spljoštimo krivu” ili se kaže, mere ograničenja kretanja u svrhu “peglanja krive”.
Pošto smo objasnili šta je funkcija i kako se funkcija grafički predstavlja, lako možemo objasniti i pojam “peglanja” ili “rastezanja” krive.
Pojam “peglanje” signala se često žargonski koristi i u elektronici, gde za cilj ima sprečavanje ili ublažavanje brze promene vrednosti nekog signala. U slučaju širenja virusa Covid-19 “peglanje krive” ili “spljoštanje krive” odnosi se na usporavanje rasta broja zaraženih kako se ne bi prešao prag koji predstavlja kapacitet zdravstvenog sistema. Kako to grafički izgleda:

U slučaju uspešno sprovedenih zaštitnih mera, funkcija rasta broja zaraženih ima mnogo blaži rast i samim tim daje veće šanse zdravstvenom sistemu da se izbori sa brojem ozbiljno obolelih i smanji broj smrtnih slučajeva.
Matematičke simulacije
Matematika nije Medicina ili Epidemiologija, ne može da Vas izleči ili da pobedi neki virus, ali može da uz pomoć matematičkih modela i matematičkih simulacija pruži jasniju sliku šta možete da očekujete u različitim scenarijima.
Matematički model predstavlja manje ili više uprošćenu predstavu stvarnih veza između veličina koje karakterišu neki proces i odražava najvažnije karakteristike procesa. Tako se dobrim matematičkim modelom smatra onaj koji odstupa od realne slike u granicama tolerancije, a pri tome nije tako kompleksan da bi određivanje brojnih vrednosti parametara koji figurišu u modelu (kao i njegovo rešavanje) bilo vrlo otežano ili nemoguće.
Sajt https://www.washingtonpost.com objavio je Korona simulator kako bi čitaocima vizuelno, na osnovu matematičkih modela, predstavio širenje virusa uz korišćenje različitih mera. Treba razumeti da:
- svako može biti prenosilac virusa, iako nema simptoma,
- virus se vrlo lako prenosi u bliskom dodiru sa ljudima ili površinama koje imaju virus
- virus se nalazi neko vreme u telu domaćina (i to vreme se domaćin smatra zaraženim), posle određenog vremena, u najboljem slučaju, imuni sistem uspeva da se izbori sa virusom i virus nestaje iz tela domaćina kada se on smatra izlečenim. Izlečeni ljudi ne mogu ponovo oboleti od istog virusa ili ga preneti (biti zarazni).
Kako izgleda šitenje virusa ukoliko se nikakve mere ne odrede ili ne poštuju?
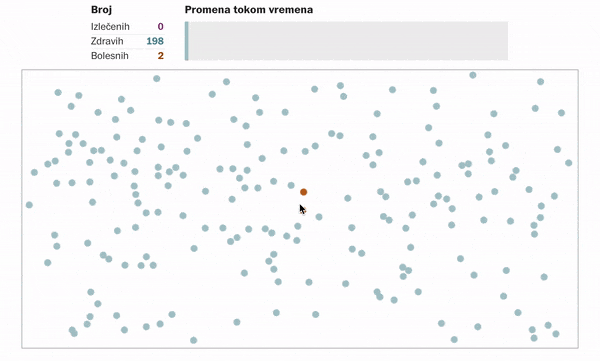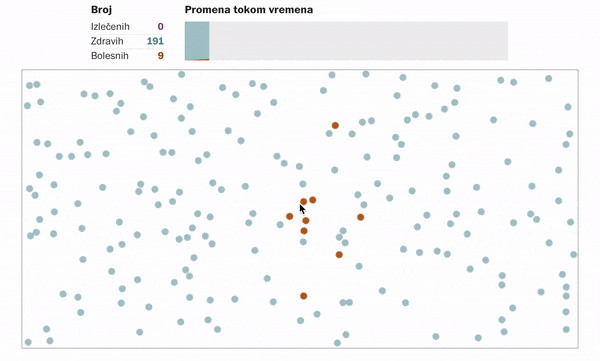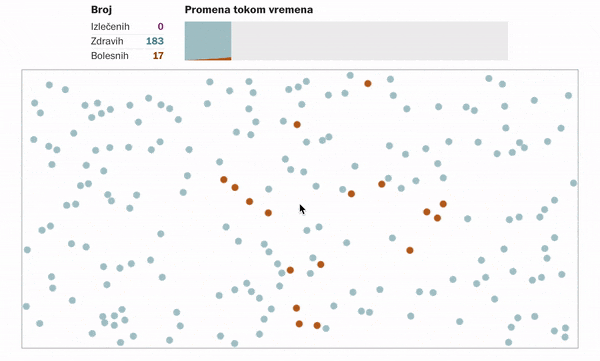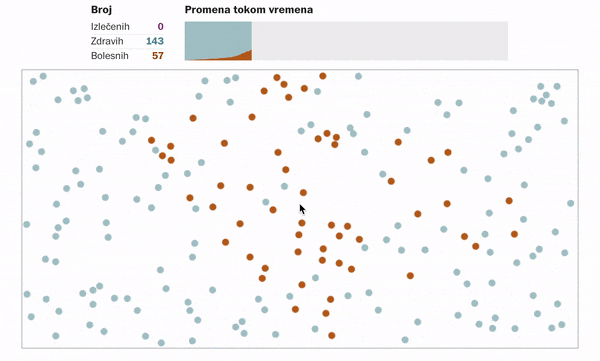
Ukoliko se ljudi distanciraju, tj. ostanu u svojim domovima u nekom vidu samoizolacije. Primenjuju propisane higijenske mere, ne kreću se, sprečavajući tako kontakt sa potencijalnim zaraženim osobama, onda to izgleda ovako:
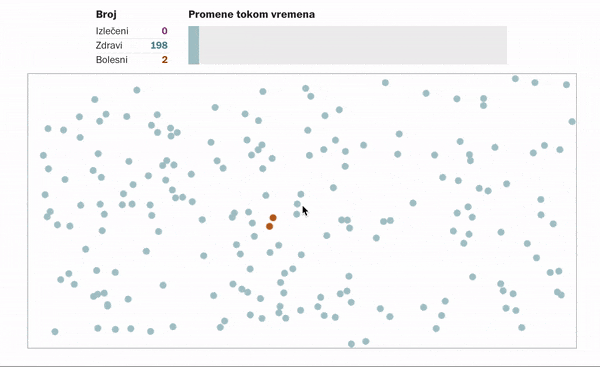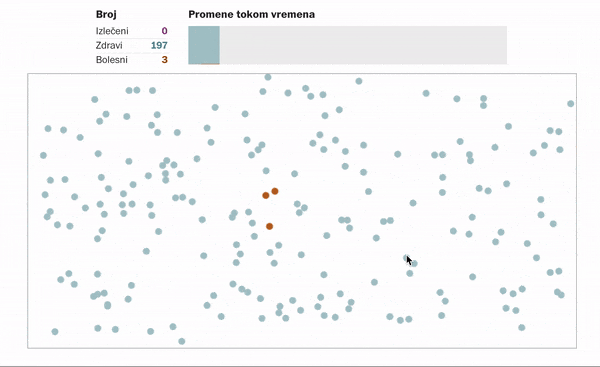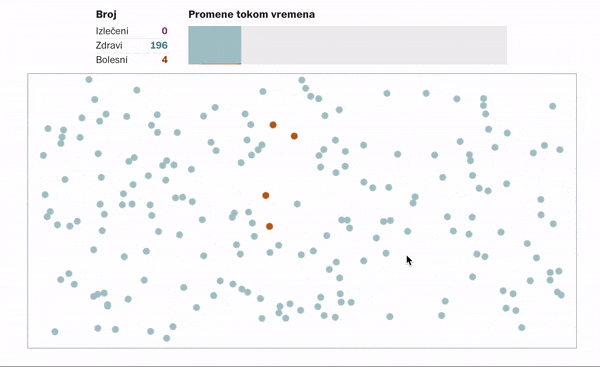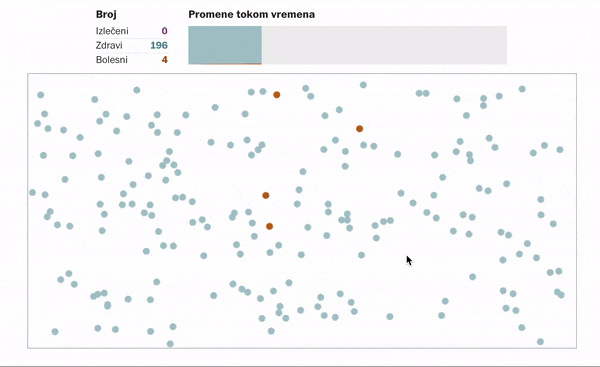
Detaljnije simulacije možete pronaći na sajtu https://www.washingtonpost.com
Dexter’s IT laboratorije su danas (16.03.2020.) obustavile nastavu u svim gradovima u kojima rade. Iako se naša nastava odvija u grupama od 4 do 8 polaznika u klimatizovanim prostorijama, koje se detaljno čiste svaki dan, želimo da damo svoj doprinos u borbi za usporavanje broja rasta zaraženih i uspešno “ispeglamo” krivu funkcije.

Čim se stvore uslovi, nastavićemo sa svim našim aktivnostima i nadoknaditi propuštene časove.



